- Knapsack Problem
어떤 배낭이 있고 그 배낭 안에 넣을 수 있는 최대 무게는 K이다.
배낭에 넣을 수 있는 N개의 물건이 각기 다른 가치 V를 가지고 있으며 각 물건마다 다른 무게 W를 가지고 있을 때,
배낭이 최대한 가치 높은 물건들을 담을 수 있는 조합을 찾는 문제이다.
위 문제를 어떻게 접근해야 할까?
브루트포스 알고리즘으로 접근하게 된다면, 그 물건을 넣었을 때와 안 넣었을 때의 모든 조합을 확인해봐야하기 때문에 O(2^n)이 걸리게 된다.
그리디 알고리즘도 옳지 않다. 최적의 해를 구할 수 없다.
그래서 이 문제는 DP로 접근해야 한다 !
하지만, 막상 DP로 풀려고 하니 식을 도출하지 못했다. 그래서 단계별로 식을 도출해보려고 한다.
우선 위에서 말했듯이 우리가 선택할 수 있는 방법은 2가지다.(그 물건을 넣을지 말지)
물건을 넣었을 때, 가방무게가 초과되는 상황엔 물건을 넣지 않는 것 밖에 없다는 것도 고려해야한다 !
조금 더 생각해보면 다시 새로운 2가지 조건으로 세울 수 있다.
1. 새로운 물건을 넣지 않는다
2. 새로운 물건을 넣기 위해, 넣을 공간을 만들고(물건을 빼고) 넣는다
식으로 세우면 다음과 같다.
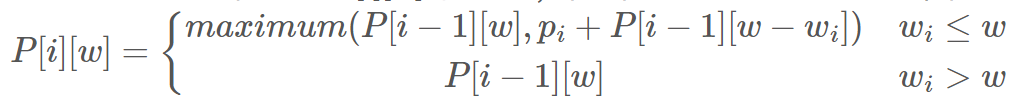
첫 번째 경우는 물건을 넣을 수 있을 때, 넣지 않거나 현재 물건을 넣기 위헤 넣었던 물건을 빼었을 경우에 현재 물건의 가치를 더하는 것 중 최대
두 번째 경우는 넣을 수 없어서 이전 값을 가져온 경우이다.

대충 이런 느낌으로 흘러가는 듯
하지만 이는 쓸데없는 계산까지 하게 되지 않나 싶다(?) 배낭의 용량(w)만큼 dp table을 생성하기 때문에, O(N*W)의 연산을 하게 된다. W가 클수록(N에 가까워질수록) N^2이나 다름없는 것..!
knapsack의 전형적인 문제를 풀어보자.
https://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
"""
문제 : 골드5 평범한 배낭
"""
n,m = map(int, input().split()) # 물품 수/ 용량
dp = [[0]*(m+1) for _ in range(n+1)]
for i in range(1,n+1):
k,v = map(int,input().split())
for j in range(1,m+1):
if j-k>=0: #넘치지 않으면
dp[i][j] = max(dp[i-1][j], dp[i-1][j-k]+v)
else:
dp[i][j] = dp[i-1][j]
print(dp[n][m])위 공식대로 다음과 같이 풀 수 있다. 하지만 229220KB / 4648ms 메모리/시간이 걸리게 된다.
ㅠㅠ 맞긴 했지만, 솔직히 너어무 비효율적아지 않나 싶어서 다른 사람들이 제출한 코드 중에서 메모리와 시간이 적은 코드를 살펴보았다.
메모리 : 35108 / 시간 : 2096 코드
# 다른분 코드 참고
from sys import stdin
input = stdin.readline
N, K = map(int, input().split())
WV = []
for _ in range(N):
w, v = map(int, input().split())
WV.append((w, v))
dp = [0 for _ in range(K+1)]
for w, v in WV:
for i in range(w, K+1):
if dp[i-w] < dp[i] + v:
dp[i-w] = dp[i] + v
print(max(dp))dp table을 굳이 2차원으로 만들 필요가 없고, 나는 조건문을 통해서 인덱스가 (-) 되는 것을 막아줬는데, 그럴 필요없이 w부터 k+1까지 반복을 돌리면 되는군..
'PS' 카테고리의 다른 글
| [소프티어] 징검다리 -level3 (1) | 2023.12.30 |
|---|---|
| 백준 양 파이썬 / sol (0) | 2023.12.19 |
| [프로그래머스] 숫자 변환하기 파이썬 (0) | 2023.08.26 |
| 이분 탐색(Binary search) 개념 (0) | 2023.03.25 |